Minesweeper solver
Table of Contents
1 Description
A minesweeper solver combining several approaches. Also includes an actual minesweeper game with a text-based GUI.
On this page I make available the source and binaries for windows and Linux. Furthermore, I describe my automatic minesweeper solver and present animations of it in action.

Figure 1: An example of the minesweeper gaming being automatically solved.
2 News
- 25 Jan 2012: Initial web page.
4 Downloads
- minesweeper-solver.zip Windows 32bit
- minesweeper-solver.tar.gz Linux 32bit
5 Playing minesweeper (POSIX-friendly method)
To play a game of minesweeper follow these steps:
5.1 Start a new game using ./minesweeper
$ ./minesweeper -n -b 0 game.txt
The argument '-b 0' is the easiest predefined board. The predefined
boards are:
- 8x8 grid with 40 mines (beginner)
- 16x16 grid with 40 mines (normal)
- 30x16 grid with 99 mines (expert)
- 78x21 grid with 450 mines (insane)
5.2 Open the file game.txt in a text editor and make some moves.
An example of a game.txt file is:
Minesweeper 8x8 grid with 10 mines ........ ........ ........ ........ ........ ........ ........ ........ Solution encrypted with seed 1327442006 8 34?1.1 !32? !31 833 3315 1 2!275* *5.4826? 28?88?8. 3?13!212 425!*.*
To make a move edit the first grid of '.'s to either a '?' if you
think tile is not a mine or a '!' if you think it is.
For example, we could replace a random '.' with a '?':
........ ........ ........ ........ ....?... ........ ........ ........
5.3 Process your input
We then process our input from game.txt using minesweeper:
$ ./minesweeper -v game.txt
This changes the game.txt file by replacing '?'s with numbers
signifying how many bombs surround that tile.
The first grid of our game.txt file now looks like this:
........ ........ ........ ........ ....*... ........ ........ ........
This means we have hit a bomb and lost the game. Or we could just
replace the '*' with a '!' and pretend it never happened.
5.4 Continue playing
Continue editing the game.txt file by replacing '.'s with '!'s
or '?'s, and processing the game.txt file.
To apply the automatic solver use minesweeper_solver:
$ ./minesweeper_solver -v game.txt
The automatic solver will replace as many '.'s as possible. If the
solver cannot make any moves it will make a guess.
6 Playing minesweeper (human-friendly method)
There is also text-based GUI to play minesweeper which can be started by runnning:
./minesweeper_curses
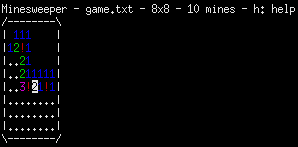
Figure 2: Human-friendly minesweeper.
6.1 Play minesweeper
Move around with the arrow keys, mark mines with space and mark not-mines with enter.
Start new games by pressing '0', '1', '2' or '3'.
Start automatically solving the game by pressing 'a'. More keys are
explained in the help menu (accessed through 'h').
7 Solving minesweeper
The minesweeper solver is uses four different methods to solve minesweeper:
- Propagate knowns and unknowns
- Make an assumption and try to prove it false
- View the board as a constraint satisfaction problem
- Guess
7.1 Propagate knowns and unknowns
This method searches for two simple situations:
- When a tile is surrounded by x mines and where x mines have been marked on neighboring tiles. In this situation we can mark the unknown neighboring tiles as being not mines.
!.. !?? .1. -> ?1? ... ???
- When a tile is surrounded by x mines and where the sum of the unknown neighboring tiles and the neighboring tiles being mines is x. In this situation we can mark the unknown neighboring tiles as being mines.
!2. !2! 132 -> 112 1. 1!
This method works by stepping through all tiles and, when either of these situations occurs, mark neighboring tiles. Continue to step through all tiles until a complete search of the tiles did not find either of the situations.
7.2 Make an assumption and try to prove it false
This methods assumes a unknown tile either is or is not a mine. We then use the previous step to propagate knowns and unknowns. If we end up in an invalid state, we know the original unknown tile is the opposite of our assumption.
An invalid state is a game that contains a situation where a tiles indicated number of neighboring mines is in conflict with the actual neighboring tiles. There are two such invalid situations for a tile:
- A tile has no unknown neighbors and the indicated number of neighboring mines is not equal to the number of actual neighboring mines.
- There is a greater number of actual neighboring mines than the indicated number of neighboring mines.
... Board 111 .?. Assume (0,1) is not a mine 111 !?! Propagate knowns and unknowns 111 (1,1) is invalid as it has 2 neighboring mines ... !.. !?? 111 -> 111 -> 111 -> Invalid state for tile (2,1)
This method works by assuming every unknown tile is both a mine and not a mine. When this step gives us new information, we propagate knowns and unknowns and. We continue these steps until no assumptions were proven false.
7.3 View the board as a constraint satisfaction problem
This method iterates through all permutations of unknown tiles being set as a mine and being set as not a mine. If a specific tile is always either a mine or not a mine for all valid permutations, we know that the tile is or is not a mine, respectively.
This is the solution mentioned on Wikipedia's Minesweeper page.
This step can solve situations our previous steps cannot. An example of this is (from Wikipedia):
1. 12. ...
There are 5 unknown tiles (.). This means there are 25 = 32
permutations. Of these permutations, 4 lead to valid boards.
0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0
The fifth number in these 4 permutations is always 0, meaning not a
mine. This, in turn, means we now know one of the tiles is not a mine:
1. 12. ..?
This method has an exponential running time in the number of unknown tiles. To minimizes the number of unknown tiles we separate them into clusters. Tiles in different clusters can not affect each other, and can therefore be solved separately from each other. This optimization lets us go from 10 unknowns (210 = 1024 permutations) to 2 * 5 unknowns (25 + 25 = 64 permutations). This optimization, however, is not enough. We also have to ignore clusters with more than 15 unknown tiles.
7.4 Guess
If the previous methods cannot give us the answer, guessing is all that is left.
A guess is defining a tile as not being a mine. Making the guess involve these considerations:
- The number of neighboring non-mines.
- The number of neighboring unknowns.
- The number of neighboring mines.
- The chance of the tile not being a mine.
- Whether knowing a tile results in further propagation (from step 1).
The chance of the tile not being a mine is based on either:
- The number of unknown tiles versus the number of mines left in the game.
- The worst chance based on neighboring tiles with a defined number of neighboring mines.
I converted these 5 considerations to values between 0 and 1 and gave each tile a score.
score = number_of_neighboring_non-mines * 0.3 +
number_of_neighboring_unknowns * 0.1 +
number_of_neighboring_mines * 0.3 +
chance_of_not_hitting_a_mine * 2.5 +
lead_to_propagation * 1.0
I modified these values until I stopped noticing particularly bad guesses.
8 Animated gifs of the automatic minesweeper solver
8.1 Beginner board, 8x8 grid with 10 mines

Figure 3: Gives some insights into how guessing works.
8.2 Normal board, 16x16 grid with 40 mines

Figure 4: Further presents guessing.
8.3 Expert board, 30x16 grid with 99 mines

Figure 5: Hits 2 mines.
8.4 Insane board, 78x21 grid with 450 mines
9 Making the gifs
This section explains how to take screenshots in an automatic fashion and how to combine them into a animated gif.
- Get window id of a terminal by running
xwininfoand clicking the terminal window. - Take screenshots of the terminal by running:
import -window 0x3000024 screenshot_001.png
- Make the screenshots into a gif using Imagemagick:
convert -delay 50 -loop 0 screenshots_*.png animated.gif
I included this behavior into minesweeper_curses. To activate it,
pass the argument: '=-w WINDOW-ID'.